Cruise Control for LLM Training

Set a target information ratio (S*). SCU maintains it automatically—reducing loss and time‑to‑target.

3B — BPT
−10.6%
3B — Perplexity
−12.6%
Time‑to‑Target
≥10% fewer steps*
*goal for 7B+ validations; see roadmap below
Book a Demo See Validation View Models

How it works

Deterministic Optimization

Traditional LLM training relies on expensive, brute‑force searches for optimal settings. It’s alchemy.

The SCU introduces engineering rigor. We apply proven control theory—the mathematics that stabilizes airplanes and power grids—to the unstable dynamics of LLM training.

SCU uses a closed‑loop feedback system to dynamically adjust training parameters in real‑time, ensuring stability and maximizing efficiency without manual intervention.

Target: S = ParamBPT / (DataBPT + ParamBPT)
Update: λ ← λ · exp(−(Kp·error + Ki·I)), error = Ŝ − S*
ParamBPT: quadratic term vs N(0,σ²), nats→bits, normalized by fixed N

PI loop regulates information budget. No manual tuning needed.

Prior Art & What's New

  • Control Theory in ML: Prior work uses PID for process knobs (e.g., learning‑rate scheduling) or targets KL‑divergence (ControlVAE).
    • How SCU is Different: We control an intrinsic information ratio S (ParamBPT/(DataBPT+ParamBPT)) and actuate the loss via λ using a bounded PI controller (with anti‑windup), holding a target information budget in real time.
  • Information‑Theoretic Regularization: MDL used for post‑hoc selection/pruning; the Information Bottleneck adds a static penalty.
    • How SCU is Different: We transform MDL into a real‑time, differentiable target inside the training loop, dynamically meeting a precise budget.
  • Classical Regularization: L1/L2 (weight decay) relies on a manually‑tuned, static λ.
    • How SCU is Different: We replace static λ with closed‑loop control that maintains S within a target band, eliminating manual sweeps.
  • Hyperparameter Optimization (HPO): BO/Hyperband/PBT search the outer loop with many trials.
    • How SCU is Different: Inner‑loop control finds the operating point within a single run—reducing steps/GPU‑hours while improving stability.

Results

Llama-3.2-1B Results

Metric Cross-Entropy Baseline SCU Improvement
BPT 3.920 3.676 −6.2%(p<0.001)
Perplexity 15.14 12.78 −15.6%(p<0.001)

Llama-3.2-3B Results (NEW)

Metric Cross-Entropy Baseline SCU Improvement
BPT 1.830 1.635 −10.6%(p<0.001)
Perplexity 3.56 3.11 −12.6%(p<0.001)

Mechanism scales: Consistent improvement at 3B parameters

Ablation: Adaptive PI Control vs Fixed λ

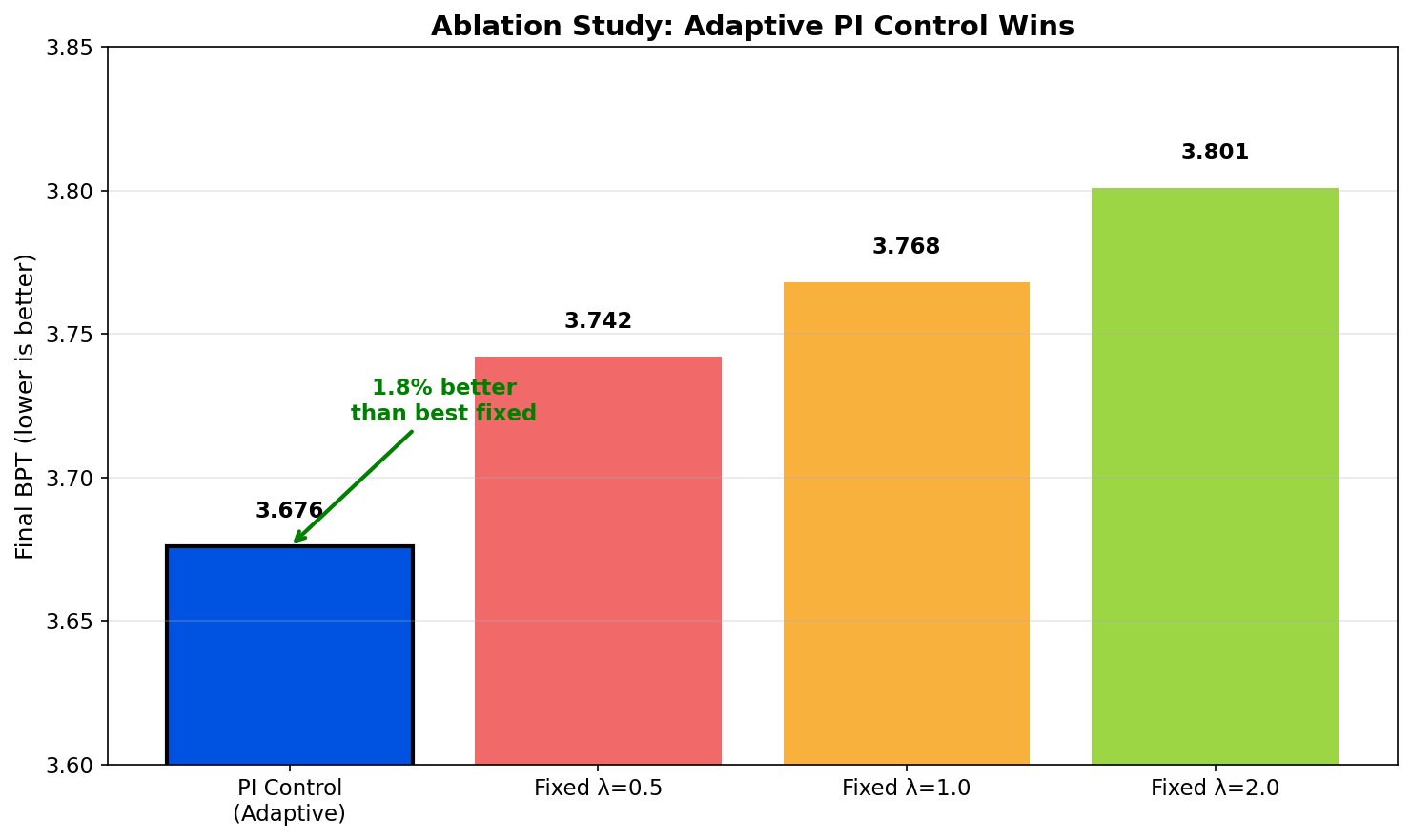
Final BPT comparison: Adaptive PI vs fixed lambda values

Fig. 2 — Adaptive PI achieves 1.8% better BPT than best fixed λ

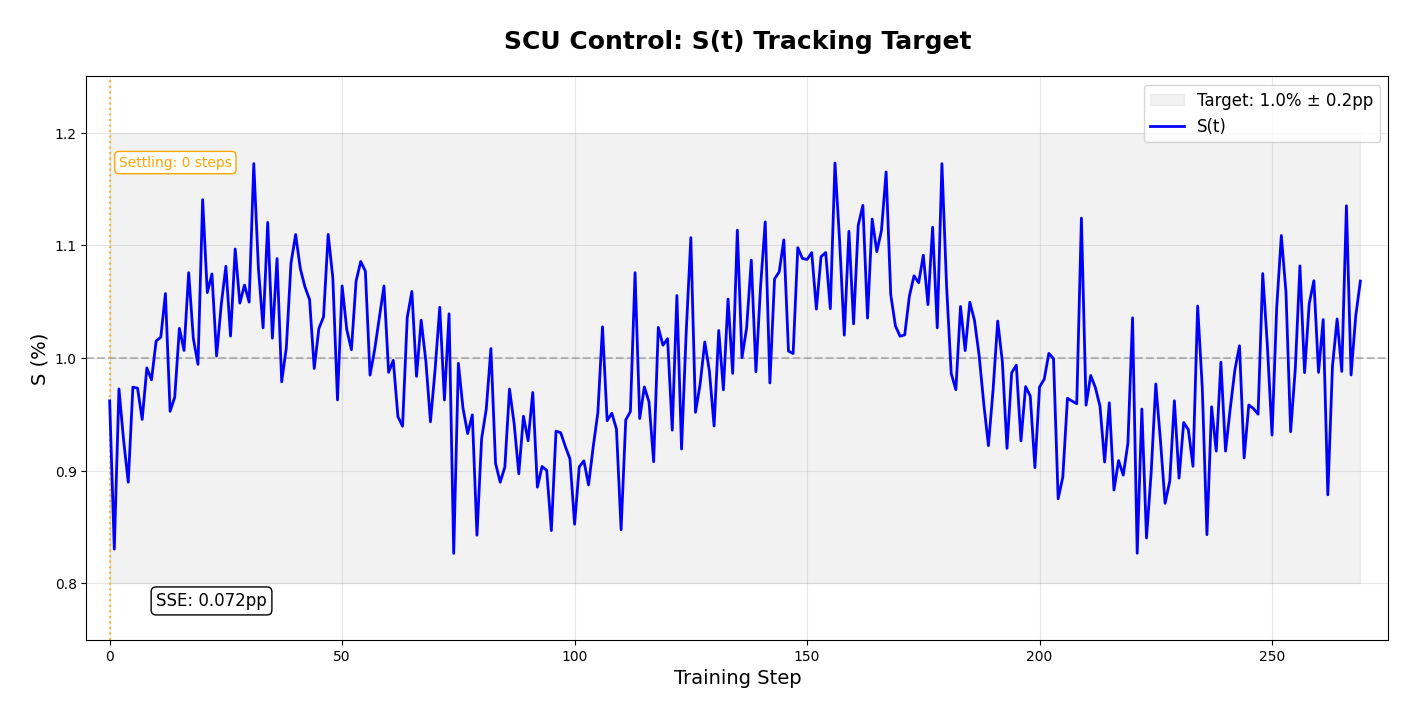
S-ratio oscillating around target showing active control

Fig. 3 — S(t) oscillates around target, showing active PI control

Key Finding: Fixed λ requires extensive hyperparameter search. Adaptive control finds optimal regularization automatically.

Validation Roadmap

PHASE A - READY NOW

7B Smoke Test

Duration
72-96 hours
Resources
32-64 H100s

Target: ≥10% faster time-to-target perplexity vs tuned baseline

Deliverable: Public reproducibility package with full telemetry
PHASE B - NEXT

Scale Validation

Duration: 3-7 days
Resources: 32-64 H100s
Models: 7B/13B

• Replicate with 2-3 seeds for variance analysis
• Measure step-time overhead (<1-2%)
• Ablate S* schedules and optimizer interactions

PHASE C - FUTURE

70B Production Validation

Duration: 30 days
Resources: 64-128 H100s (IB)
Impact: 10-15% efficiency gain

• Full pretrain segment or high-quality LoRA
• Joint case study with compute partner
• Target: Validate cruise control mechanism at production scale

Economic Impact: At US$1B training scale, 10–15% efficiency = US$100–150M saved annually

Validation & Reproducibility

Validated Performance

1B Model: -6.2% BPT, -15.6% perplexity
3B Model: -10.6% BPT, -12.6% perplexity
View models on HuggingFace →

Open Source

Complete implementation available on GitHub. LoRA adapters on HuggingFace. Interactive Colab notebook for testing.
GitHub repository →

Technical Innovation

First stable application of PI control to neural network regularization. Maintains target information ratio automatically throughout training.

Patent Pending

U.S. provisional filed (Sep 2025) covering the closed-loop control system for automatic regularization during training.

Independent Verification

All results reproducible with provided code. Seeking partners for 7B+ scale validation.

Open Research Direction

We're investigating whether there is a simple "natural operating point" for the target S* that depends on model size (M), training tokens (T), and data domain (D)—i.e., a compact relation S* ≈ f(M, T, D). Today we select S* empirically (≈1% at 1B, ≈2.9% at 3B in our setup); the goal is to predict S* from first principles and remove tuning entirely.

📚 Free for academic research under AGPL-3.0. Commercial use requires a license—contact us for terms.

Get Involved (7B+ Welcome)

Validate at larger scales, try small S* targets, and share observations (stable S* band, final BPT/ppl). Please include model size (M), tokens (T), domain (D), S* target, Kp/Ki, σ, steps, and results.

Academic/research collaborations welcome under AGPL-3.0. Corporate partnerships require commercial licensing.

The Legacy of Information Theory

Shannon Labs builds on the foundational work of Claude Shannon and the innovative spirit of Bell Labs.

Claude Shannon

Claude Shannon

Father of Information Theory (1916-2001)

Established the mathematical foundations for digital communication and computing in 1948 with "A Mathematical Theory of Communication."

Ralph Bown

Ralph Bown

Director of Research, Bell Labs (1889-1971)

Hunter's great-grandfather. Announced the transistor at Bell Labs in 1948, revolutionizing electrical control and enabling the digital age.

Continuing the Mission

Hunter Bown, Shannon Labs Founder and great-grandson of Ralph Bown, applies these foundational principles to modern AI challenges.

Just as the transistor enabled reliable control of electrical current, the Shannon Control Unit enables reliable control of information flow in neural networks.

Strategic Engagement

We will calculate the optimal information ratio for minimizing perplexity and bit per token, and our PI controller maintains it automatically throughout training as the system moves between states of increased and decreased entropy.

For organizations spending billions on AI infrastructure, SCU represents US$100M+ in annual savings. We're engaged with leading compute providers for validation at scale.

Book a Demo Email

Reproduce it

📋 Licensing

Open Source (AGPL-3.0)
  • Research & education ✅
  • Open-source projects ✅
  • Must share modifications
Commercial License
🤗 Hugging Face Models 📔 Open Colab 
pip install transformers peft accelerate torch

# Load adapter:
# base: meta-llama/Llama-3.2-1B
# adapter: hunterbown/shannon-control-unit

Adapters inherit Meta Llama 3.2 license; SCU code AGPL-3.0 (commercial licenses available).

Reproduce in one command

python scripts/eval_bpt.py --texts data/val.txt \
  --base meta-llama/Llama-3.2-1B \
  --adapter hunterbown/shannon-control-unit

Strategic Engagement

The Shannon Control Unit enables automatic regularization control for LLM training. We're validating at production scales with organizations that spend $1B+ annually on AI infrastructure.

If your organization spends $1B+ annually on AI training, contact us.

Book a Demo Email Instead